2003年12月28日 建築あそび記録
菅野裕子 さんによる 建築と音楽
p−1 p−2 p−3 p−4 p−5 p−6
p−7 p−8 p−9
1934年にはロイ・ハリスという人が、弦楽四重奏とフルートの為の4分20秒という曲を作曲して、曲のタイトルに時間が入っていたり、その・・20年後1954年にジョン・ケージの有名な4分33秒というのがあるんですが、
このように近代的に時間が計られるようになると、そいいう記述とか指示が、曲の中に入ってくるのは面白いのではないかと考えたんですが、それに対して空間はどうなのかというと・・建築家のパラディオの本では 「私は都市に固有な尺度ブラッチョとかピエーデという 今でいうメートルとうようなものなんですが、それをなるべく用いないようにした。というのがこの尺度が都市や地方によって異なるから」と書いています。つまり地方の単位を使ってもそれは共通の尺度にならないと考えたからなんですが・・・
つまり時間の尺度が1日に24時間という長さ 色んな地方によって共有出来るのに対して 空間の尺度というのは地方性があるのであまり当てにならないから、絶対的なものを計る正確な根拠がないので・・こういう視点で空間と時間を比較すると、空間と時間があまりにも状況が違うので・・一寸 難しいナー というふうに行き詰まって・・これはこれで一寸保留になっています。
その頃いろいろ調べている時にルネサンス時代の神学者とか天文学者が宇宙の無限な空間について色んな本を書いていたり、様々な発言があって、そういうもの抽象的な空間を考えるのに 関係有るんじゃないかと思って、読んで・・でもそれも読むと面白いんですけど、建築家にとっての抽象的な空間概念というのは恐らく宇宙空間とかそういうものじゃなくて、もう少し身近なものの大きさなので一寸それは違うんじゃないかということも考えました。
で大きさの概念がどういうモノかを考えてみると、例えば二つの大きさを比較するときに、自分の目の前にレコードとCDがあるとして、その大きさを比較すると考えたら、目の前のレコードは黒くて、CDは銀色だったりとか・・レコードには溝があってとか・モノにある属性がいろいろあるんですが、大きさを比較する時は頭のなかで、他の色とか形とか、材質を一回リセットして、その大きさだけを頭で取り出して比較するということになると思ったので、その時に大きさ概念というものが、まずこの思考の中にあると考えました。
それからまた一寸話は飛ぶんですが、ガリレオがどういうふうに天体を観測していたかということを読んだ時に、ガリレオが宇宙の衛星の間隔を木星の半径を単位にして読んだというのを知りました。
ガリレオは天文学で、凄く広い宇宙について考えて衛星と衛星の間の長い距離や空虚な天体というものを認識していたのですが、その空虚なものも実体の倍数で計測していた。木星という実際にある衛星の倍数で計測していたというのが・・なんとなくあぁそうなのか・・不思議だナーと思ったんですが・・・
これがセルリオという人の16世紀の建築家の本なのですが、こういうふうにこの当時の人は見えない空間というのを何か意識して、それをこう・・グリッドにして書いているようなんですが
●スライド

なんですが、これを見ると分かるのですが柱が有るところと、それ以外の空間というのはきっぱりと分けられて、補助線が引かれています
●スライド

これはパラディオの図面なんですが、これここに何が書いてあるかというとここからここまでの長さが記測されているのですが・・空白と壁とその間というものがハッキリと分けられて数字が書かれています
●スライド

これはパラディオの別な図面なんですが、ここにも小さな数字が書いてあるのですが、ここの一つ一つのパーツが分けられて計測されています
●スライド
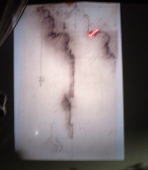
これはボッロミーニのスケッチなんですけれども ここが建築の形であって、それ以外のところは分かれていて 斜線が引かれていたりして、ハッキリと実体とそれ以外の所が分けられています。 建築を作るというときには、物が有るところと無いところというのは 全然別の所で物を作るわけだから、 こういう考えというのは凄く当たり前のようにも考えられるんですが・・
●スライド

これは1800年のデュランという人の書いた図面なんですが、この頃になるとこの補助線というのがどいいう所に発生しているかというと、柱の中心に補助線が来ていて、補助線と補助線の間の距離をもし計ったとしたら、ここに一寸柱の部分が有って、ここは空白で、という風に、実際と空虚の部分が混ざった寸法になってしまいます
昔だったらこの柱がどれくらいの幅で、間がどれくらいと計っていたのが、デュランの図面ではそれを統合してグリットを想定して書くようになったという違いがあります。
●すらいど

これもおなじくデュランの図面です。こういうふうに補助線が入っています
●スライド
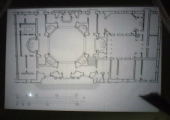
これもさっきあったサンタニエーゼの建築の図面を現代に書いたモノなんですが、ここにメートルが入っていて、ここにフィートが入っているんですが、このメートルというのを使ってこの人達は設計したわけじゃないので、これは絶対的な大きさを示すためにここに入っているもので、建築の一つ一つの長さを作った尺度とは違います。
もちろんこれで計ることはできるんですが、さっきまでの図面みたいに、ここからここ、ここからここと考えるんじゃなくて、モット透明な空間というのかなー・・広がりの中にこの建築があるというように書かれていて・・チョト図面の書き方が変わってきている。
ダンダン抽象的な表現というか、客観的な表現になっていると思うのですが、そいいう感覚とか考え方というのはどういうふうにして生まれたんだろうと考えました
ガリレオとかセルリオやパラディオというのは大体16世紀から17世紀の同じ時代なんですけども ガリレオは凄く広い宇宙の事を考えていて、セルリオやパラディオは建築だから身近な所のものを考えていたんだけれども、それでも物を計測する時には、その柱の太さだとか、実際の物で計測していたところは共通していているので、なにか同時代性があるんじゃないかということと、巨大な物でも小さな物でも類似の発想があるんじゃないかと、いうふうにそこで考えました 。
・・時計が・・時計ないです・・ 時間を気にしている菅野 時計を探している
・・単位について一寸また考えたんですが、普段ものの大きさや時間の長さを私達が測るときには 共通の単位を私達は使っていて、例えば秒だとか時間だとかメートルだとか、そういうものですけども、その単位が共通だから、廻りの人や遠く外国の人だとか、そういう人にも物の大きさや時間の長さを正確に伝えることが出来ると思います
例えばここにティシュペーパーぐらいの大きさが有るとします、その大きさをどうやって記述するかというと、高さが10センチで幅が20センチで奥行きが10センチの箱があったとすると、もう一つの言い方としては例えば高さが10センチで、幅は高さの2倍で奥行きは高さに等しいと言うことも出来ると思います。
最初の言い方と言うのは、センチメートルという物を単位にして大きさを示した場合で、それに対して幅は高さの2倍だとか奥行きは高さに等しいという言い方というのは、その箱の各部分の中の相対的な関係を表しているとうことになると思います。
先の10センチという表現が絶対的であるのに対して、2倍とか等しいという表現は相対的なんですが、それと同時に単位に対してもう少し考えてみると、・
単位によって示される大きさの性質とか意義というのは、基準とされる単位に関連していて、例えば空間芸術である建築にとっては基準の単位は、空間という次元におけるメートルなどの大きさであるのに対して、時間芸術である音楽にとっては何秒とか、時間的な長さです。
またメートルを単位として天井の高さとか壁の厚さ等の建築の部分を計測すれば絶対的な大きさというふうに考えられますが、例えばこの部屋の壁の厚みを一つの単位としてそれによって天井の高さだとか、部屋の広さを計測したとしたら、それはこの部屋の中の大きさの相対的な関係になる、と考えられます。でも本当によく考えてみると、大きさと言うのは言葉とか数値に示した時点で全てが相対的になると考えました。
といのは何かの大きさを言葉とか、数値で表すというは結局それは比較する尺度、との相対的な関係でしかなくて 絶対的な大きさ というのは大きさそのものでしかあり得ないというふうに考えられて、メートルで計るということはメートルという尺度の相対的な関係で、そのメートルという関係が皆に共有しているから共有している者同士が伝えられた何メートルという数字を見ることによって、絶対的な大きさをそこで知ることが出来るから・・・その大きさは言葉で表現したら相対的なんだけど、相対的な大きさとして伝えることによって絶対的なものが伝えられる・・
・・なんか分かるとおもいますが・・笑い・会場微笑む・・
その時の感じというのが抽象的なもので、どういう意味かというと。普通何メートルといったとき、例えばここが2メートルとか背が何センチとかいう時は そのメートルとかセンチというのは何であるかというのは普通考えている人はいなくて、普通の人にとってはある大きさ・・しか意味していない。
メートルというのはいつ出来たかというと、1790年にタレーランという政治家が天然物によって尺度を決めるべきだという発言を議会でして、それによってそれが切っ掛けとなって、1メートルがパリを通る子午線の北極から赤道までの長さの10の7乗分の一とそこで定められました。
つまり私達がもし1メートルとか2メートルとか3.5メートルとか言っている時は、地球の大きさを基準としてそれとの相対的な大きさ言っていることになります。
もしそれを月を基準にしたら、月との基準のメートルというのが出来るはずだと思います。
実はメートルは1960年にまたさらに定義が変わって、クリプトン原子の順位に2p10と5d5・・・これは原子核の回りの軌道だと思うのですが、その間で遷移する光波の真空中における波長の16万5、763..73 倍に等しい長さという風に定義づけられました。
次のページへ